スペースシャトルに搭載されているロボットアームでお馴染みのように， 柔軟なロボットのアームの運動を制御するには，振動も同時に制御しなけ ればならない。本研究では，このような課題に挑戦している。
＜宇宙開発とロボットアーム＞
空を飛ぶことは人類の長年の夢であった．この夢を叶えた最初の乗り物は気球であったが，当時の気球はただ空中に浮いているだけであり，高さの調節もままならないものであった．人類が初めて自由に空を飛んだのは，今からおよそ100年前の1903年のことである．このときの飛行時間はたったの12秒であった．100年経った現在では，超音速旅客機や80時間ノンストップで世界一周できる飛行機も登場した．図左はライト兄弟のライト・フライヤー号，図右はエールフランスの超音速旅客機コンコルド，図下はノンストップ世界一周を目指す，ヴァージン・アトランティック航空のグローバルフライヤー号の写真である．今や飛行機は人々の生活を支える重要な輸送手段となっており，わずか100年の間に「空を飛ぶ技術」は飛躍的に進歩した．そして，人類が空から宇宙へと目を向けて実際に宇宙へ進出することになる．
人類が初めて宇宙に飛び出したのは，ライト兄弟の初飛行から60年後の1961年のことである．当時世界の2大国家であったロシア（旧ソ連）とアメリカの競争により，宇宙開発は急速に進歩した．世界で初めて人類を宇宙へ送り出したのは，ロシア（旧ソ連）の有人宇宙船「ボストーク1号」であり，このときの宇宙飛行士であったユーリ・A・ガガーリンが語った「地球は青かった」という言葉は日本でも有名である．このときの飛行時間は１時間48分であった．その直後にアメリカが有人宇宙船「マーキュリー」を打ち上げている．人類初の船外活動もロシア（旧ソ連）が1965年に最初に成功させており，ここでもアメリカは2番手であった．アメリカは国家の威信をかけて人類を月に送り込むアポロ計画を発表し，1969年に世界で初めて成功している．図左はボストーク1号の写真，図右はアポロ宇宙船の写真である．
ここまでは2大国家の競争であり冒険の域を脱していなかったが，これ以降は宇宙に長期滞在するなど本格的な宇宙空間の利用が始まった．まずロシア（旧ソ連）が1971年に宇宙ステーション「サリュート」を打ち上げ，1973年にはアメリカが宇宙ステーション「スカイラブ」の運用を開始し，人類は軌道上でさまざまな研究を行うようになった．1975年にはアメリカのアポロ宇宙船と旧ソ連のソユーズ宇宙船がドッキングし，2大国家の宇宙開発は「競争」から「協調」へと形を変えていった．こうして，宇宙開発は国際協力のもと行われる時代に突入した． 　1982年，米国航空宇宙局（NASA）は前年に運用を開始したスペースシャトル計画に続く有人宇宙計画として，将来の宇宙環境利用および月・惑星探査のための中継基地として利用することを目的として，国際宇宙ステーション計画の概念設計を開始した．また，NASAはこの計画を国際協力により進めることとし，日本やカナダ・欧州諸国等の友好国に対して調査・研究段階から計画に参加するよう呼びかけた．1991年には，アメリカとロシア（旧ソ連）は両国間の宇宙協力を拡大することに合意，宇宙ステーション計画も国際化へと大きく前進した．その後，宇宙ステーションの公式名称は「国際宇宙ステーション」（ISS : International Space Station）とになった．下図はISSの完成予想図である．
1998年11月20日，基本機能モジュールとなる「ザーリャ」が打ち上げられ，ISSの建設が開始された．現在，日本実験棟である「きぼう」も含め，参加各国の協力のもとに2008年の完成を目指して，着々と建設が進められている．
kibou
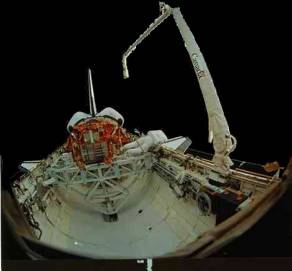
このISS建設のためには，膨大な国際協力作業とそのための準備が必要となる．また，ISSの組立とその維持のためには，船外活動（EVA：Extravehicular Activity）とロボットの分野の技術が活躍すると考えられる．船外活動では，コネクタの着脱，ケーブルの取り付け，取り外し，細かな機器の交換，ロボットアームのオペレーション支援が重要な目的である．船外活動は宇宙ステーション組立に非常に重要な技術，作業形態で，2003年12月10現在，51回318時間37分実地されている．しかし，ISS組立のためには1260時間（約200回）以上のEVAが必要とされており，今後も多くのEVAが予定されている．一方，ロボットアームの役割は，宇宙ステーションの組立，人工衛星の放出と回収，EVAではできない重い物体の移動等，およびEVAのサポートである．また，宇宙飛行士は船外活動時に手を使って構造物の外壁にそって移動するが，長距離を移動する場合にはこの方法では疲労が激しい．そこで，ロボットアームの先端に乗って動かしてもらう，あるいは必要な機器を持ってきてもらう，といったことを行う．両者を比較するとEVAは細かい作業ができるが，リスク，クルーの疲労，プリブリーズの問題がある．一方，ロボットアームはリスクが少なく大きいものも運べるが，グラップルフィクスチャと呼ばれるロボットアームがつかむための把持部がないと把持できない，細かい作業ができない，作業範囲が限られるといった問題がある． 　若田宇宙飛行士が参加した国際宇宙ステーション組立ミッション（STS-92）では，4名のEVAクルーが2人一組みになり，2回づつ計4回のEVAを行った．シャトルがISSにドッキング中に行われるEVAでは，通常1人がロボットアームの先端に足を固定して移動式の足場として利用し，もう1名は，ISS外壁の足場やハンドレールを利用して，移動し，作業を行う．ISSはとても大きく，外壁すべてをカバーできるほど足場や手すりを配置できないため，このような手段を必要とする．このように，EVA作業時には，スペースシャトルのロボットアームを操作する船内クルーとの連携が重要なため，事前に，ジョンソン宇宙センター内の無重量環境訓練施設（NBL：Neutral Buoyancy Laboratory）を使ってEVAを模擬した訓練が入念に行われている．図は第4回目の船外活動を行うミッションスペシャリストのピーター・ワイゾフとマイケル・ロペズ−アレグリア宇宙飛行士である．若田宇宙飛行士の操縦するロボットアームを足場として作業を行っている様子がよくわかる．
このように，EVAにおける効率の良い作業や，作業員の安全のためには，高速かつ高精度な宇宙作業用のロボットアームが必要となる．さらに，宇宙空間では重力の影響を考える必要のないことや，打ち上げコストを低減させるために，ロボットアームは軽量であることが望まれるようにもなった．しかし，その軽量化によりアームが柔軟化し振動が起きるという新たな問題が発生してしまった．そこで現在，フレキシブルなロボットアームの運動と振動を同時に制御することが望まれている． 　図は若田宇宙飛行士が実際に使用したカナダ製のロボットアームである．若田宇宙飛行士はこのロボットアームを非常にゆっくりと動かすことで，振動を起こさずに作業を行った．これには非常に高度な技術が必要で，訓練だけでも長い時間と高額な訓練費を必要とする．効率的な作業のためにも，短期間の訓練で安全に使用できるロボットアームの開発が望まれている．
＜アーム先端に質量の不確かさを有する柔軟アームのロバスト振動制御＞
●背景
前の述べたように，国際宇宙ステーションのような大型構造物の建造や，破損，故障した衛星を修理するために，その衛星を確保するような際により大きな力と作業範囲を持つロボットアームが使用される．このようなロボットアームの性能をさらに高めるために次のようなことが求められる．まず、作業範囲拡大ためのアームの長腕化，そして搬送コストや維持コスト低減のためアーム自身のの軽量化，そして作業効率向上のための搬送質量の増加だ． 　しかし，アームを軽量化や長腕化することは,本来剛体と考えているロボットアームを柔軟体と考える必要がある．また，ロボットアームの基本性能の一つにものを掴むということがあるが，ロボットアームが慣性中心を把持するのは困難であり，.これより柔軟なロボットアームがペイロードを掴む音ができなかった場合，低周波領域で曲げとねじれの連成振動が励起されることが考えられる．また，このペイロードの質量などが不確定な場合，その連成の度合いも不確かなものとなり，制御性能の低下につながる恐れがあるのである．
●目的
そこで，本研究ではこのようなペイロード把持による不確かな連成振動が励起される柔軟ロボットアームに対し，構造的不確かさを考慮するH∞制御器設計手法を適用し，ペイロード把持により連成振動が生じた場合でもロボットアームの運動及び振動の制御性能低下を回避する方法を提案する． まず，ロボットアームの制御性能の低下の回避を狙う構造的誤差を考慮したH∞ロバストサーボ制御器の作成方法について説明する．次に，作成した制御器を用いて制御実験を行い，その有効性を検証する．最後に，作成した制御器に様々な様々なペイロードを適用させたときの制御器の制御性能の低下と安定性が保たれているかを実験的に検証する．
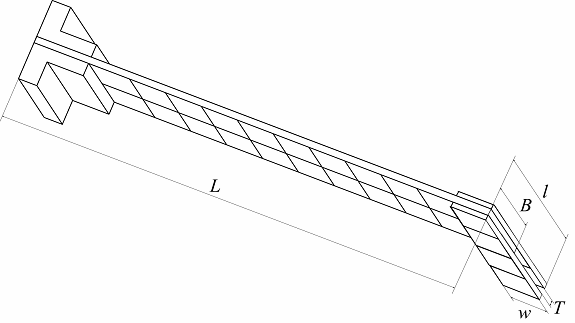
こちらが，本研究で用いる制御対象構造物になる．制御対象構造物の寸法は，長さ80[cm]，幅5[cm]，厚さ2[mm]のステンレス製で重さが718.5[g]となっている．こちらは，根元がL字プレートを介してドライブシャフトに取り付けられている． この平板構造物の先端に，ロボットアームがペイロードを把持したと考え，ペイロードを取り付ける．本研究で使用するペイロードの寸歩は、幅4[cm]，厚さ2｢mm｣で，長さを変化させたて使用する．
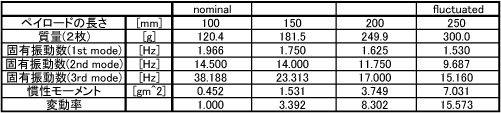
次に，ペイロードの長さの変化による振動モード形の変化について説明する．柔軟アームがペイロードを把持する際，その慣性中心を把持できなかった場合，曲げとねじれの連成振動が励起される．ここでは，把持するアームの長さが変化した場合の振動モード系がどのように変化するかを検証した．使用するペイロードは，長さを10[cm]から5[cm]刻みで4パターンで，それぞれ振動特性を得るために有限要素解析ソフトNASTRANを用いて実固有値解析を行った．また，このときのペイロードの上端回りの慣性モーメントを平行軸の定理より求めた． 　これより，質量の増大による曲げ振動の固有振動数の変化より，慣性モーメントの増大によるねじれ振動の変化のほうが振動特性に大きな影響を与えていることがわかる．
0.1[m] 0.25[m]
また，上図がNASTRANで解析したそれぞれの2次モードの結果である．これからもわかるように、ペイロードの長さが0.1[m]のときでは曲げモードだった2次モードが，0.25[m]の時にはねじれモードになっていることが確認できる．また，こ時の上端回りの慣性モーメントを調べた結果，およそ15倍の変化が確認された．本研究では，このようなペイロード把持による固有振動数の大きく変化する問題に積的に扱うこととし，制御対象を0.1[m]と0.25[m]のときとした．また，本研究では0.1のときをノミナルモデル0.25[m]の時を変動モデルと呼ぶ．
Nominal Model
1st mode 1.5300[Hz] 1st Bending mode 2nd mode 14.500[Hz] 2nd Bending mode 3rd mode 38.188[Hz] Bending and Torsional coupled mode
Fluctuated model 1st mode 1.5300[Hz] Bending mode 2nd mode 9.387[Hz] Torsional mode 3rd mode 15.160[Hz] Bending and Torsional coupled mode
こちらは，制御対象のノミナルモデル，変動モデルの有限要素解析結果である． .本研究では，制御対象モードをノミナルモデルの1次，2次モード，変動モデルの1，2，3次モードを制御対象モードとする．
●設計仕様
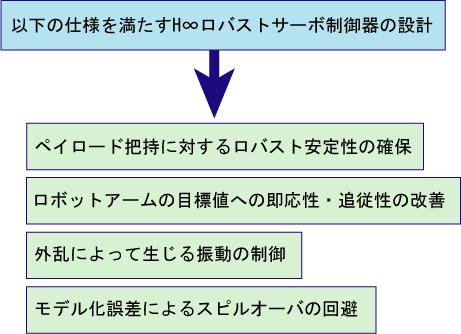
次に，本研究で作成する制御器は以下の性能を達成するようH∞制御理論を用いて作成する．まず，先ほど説明したペイロード変動に対する制御性能の低下や不安定性に対するロバスト安定性の確保，ペイロードを把持して軸を運動させることを想定した,軸の即応性や追従性の改善，浮遊しているペイロードを掴むことを想定した外乱に対する振動制御，制御対象を物理モデルにモデル化した際の高次のスピルオーバ回避などである． 本研究では，これらの性能を確保するH∞ロバストサーボ系を設計することを設計目標とする．
●物理モデル作成(nominal model)
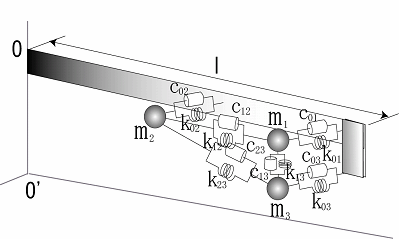まず最初に，柔軟アームを3自由度集中定数系物理モデルに低次元化する．本研究では，物理モデルを低次元化物理モデル作成法を用いて作成した．モデルの質点は各モードの最大振幅点に配置した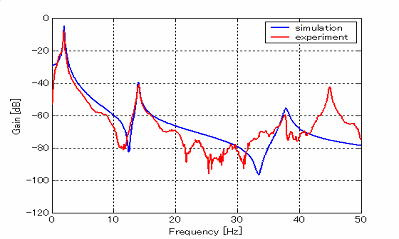． 　作成した物理モデルの妥当性を検証するために，実機とモデルの質点1の周波数応答の 比較を行った．モデルの反共振の位置にずれが生じていますが，作成した物理モデルが平板の振動特性を表現できていることが確認できる．
●物理モデル作成(fluctuated model)
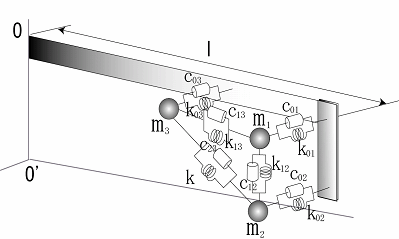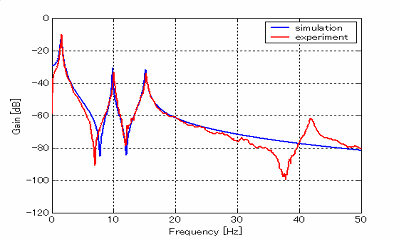同様に変動モデルも低次元化物理モデル作成法を用いて3自由度集中定数系物理モデルに低次元化した上図が，変動モデルの周波数応答の比較線図となる． これより，作成した物理モデルが実機の振動特性を表現できていることがわかる．
次に，構造的誤差の選定方法について説明する．構造的誤差とは、制御対象に生じる減衰や合成などの物理パラメータの変化を表す．この構造的誤差を抑えたい物理量として考えることで，実際のシステムに変動が生じた場合でも制御器の安定性を保つことができる． 本研究では，この構造的誤差をモデルパラメータの変化そのものと考え，この物理モデルの差を構造的誤差として制御系に組み込むことで，アームがペイロードを把持した場合でも，制御性能の低下や不安定になることを回避できると考えられる． 　本研究では，これを誤差マトリクスと呼ぶ．まず，状態量の誤差である状態誤差マトリクスΔA，制御入力の誤差である制御入力誤差マトリクスΔB，観測行列の誤差である観測誤差マトリクスΔCである．これらを構造的誤差として一般化プラントに組み込む．
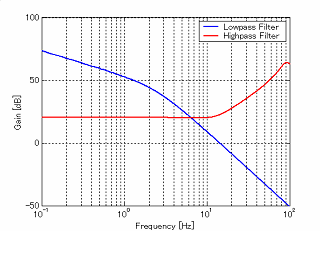次に，重み関数と外乱の選定について説明する．本研究では，即応性などの運動性能を向上させるため，重み関数として積分特性を持ったローパスフィルタを軸と目標値との誤差に作用するように配置している．これは，ロバストサーボ系設計方法の一つである重み行列を用いる方法と同一である．また，高次のモデル化誤差に関しては，制御入力電圧に作用するように配置した．また，飛来しているペイロードをつかむ際に生じる振動、つまり外乱による振動に関しては，インパルス外乱を今回は外乱として採用し，各質点に配置した．
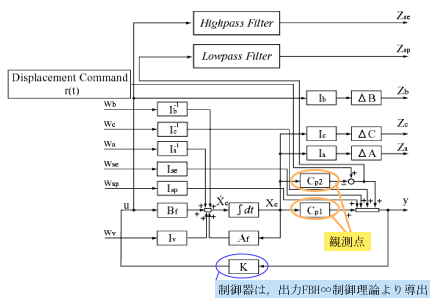
こちらが，構造的誤差と重み関数，インパルス外乱を考慮した一般化プラントになる．本研究では，観測点を根元の角度と平板の先端の加速度とする． 　また，位置決めは根元のの位置が目標値に到達することで評価し，振動は先端の加速度を抑えることで評価する． また，本研究では観測点は２この2点だけで全状態量は観測していないので，出力FBH∞制御理論より制御器を導出する．
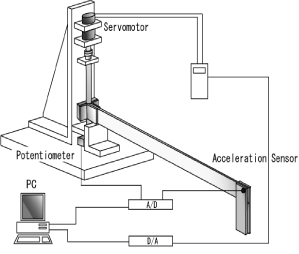
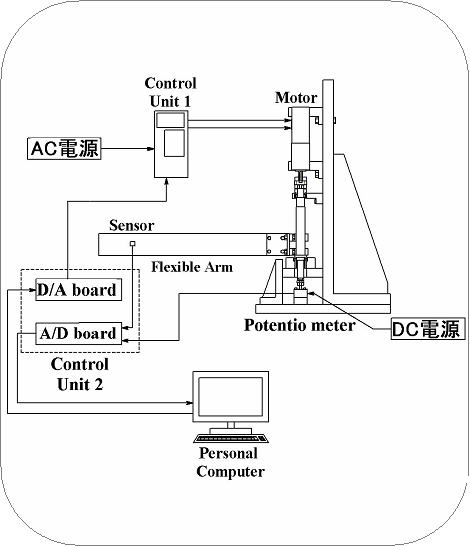
●実験装置概要
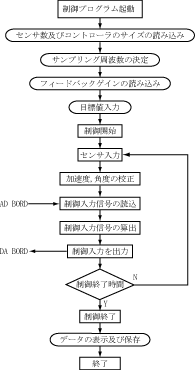本研究では制御用コントローラとしてAD/DAボードを搭載したパソコンを用いる．これにC++を用いてコントローラを作成し，そこにシミュレーションより求めたフィードバックゲインを実装し制御を行う． 次に実験の流れについて説明する．平板の先端の加速度を加速度センサで，軸の角度をポテンショメータで計測する．計測した数値はADボードを介して制御用パソコンに送られる．パソコン内では求めたコントローラと出力信号から制御出力信号を算出する．算出した値はDAボードを介してアクチュエータのアンプに送られ，アクチュエータを駆動させ平板を制御する機構となっている．また，えられたH∞コントローラはサンプリング周波数1000[Hz]として離散化した． 非構造的誤差を考慮したH∞制御理論を曲げのみが生じる柔軟ロボットアーム，曲げとねじれの連成振動が生じるロボットアームそれぞれに適用し，運動と振動を同時に制御してきた．本章の目的でもある感度関数，相補感度関数であるフィルタを用いて，追従性，振動制御，スピルオーバ安定性全てを満たすコントローラの設計が達成されたと考えられる．また，本研究では，振動制御の性能を決定するバンドパスフィルタを個別に設計した．こうすることで，希望するモードに個別に制御能力を決定することができ，加速度センサでは応答の低い1次モードに対してより大きなゲインを働かせることができ，全モード-でゲインを低減できたものと考えられる．
ペイロード把持による制御性能の検証 　　　以下の4つのペイロードをアームに取り付け，実験的に安定性を検証
N1 model (l=0.015[m]のペイロード) N2 model (l=0.0175[m]のペイロード) N3 model (l=0.020[m]のペイロード) N4 model (慣性モーメントのみ変化)
●結論
本研究では，作成した制御器に様々なペイロードを取り付けた時の制御器の安定性について検証した．フィルタのみで構成された非構造的誤差のみを考慮したH∞制御器では，制御器のベースとなる制御対象以外で安定性は補償されていない．そのため，本研究で行った様々なペイロードを取り付けた場合において，コントローラの安定性は必ずしも補償されない．実際，ノミナルコントローラに変動モデルを適応した場合，また変動コントローラにノミナルモデルを適応した場合など，変動が大きくなるにつれ，制御器の制御性能が低下しただけでなく，システムが不安定になってしまった．その点，構造的誤差を考慮する制御器では，全制御対象モードで制御性能が劣化することなく安定的に制御することができた．この方法でも，考慮されていない制御対象について安定性は保たれていない．しかし，変動の端点の状態から制御器を導出した場合，考慮されていない場合でも，制御性能に対する高いロバスト性を有することができると考えられる．しかし，変動幅の小さいとき，例えば，ノミナルコントローラに剛体モデルを適用した場合などは，H∞制御理論の持つロバスト性で，非構造的誤差のみを考慮したH∞制御器でも十分制御可能であると考えられる．