近年,磁気浮上・磁気軸受技術は盛んになってきており,最先端技術の1つに上げられている.この技術が用いられている磁気軸受は真空ポンプや工作機械等に用いられている.
磁気軸受を用いる利点を述べる.そして,最大の利点として,ロータを非接触で支持する事により機械的摩擦から解放され,高速回転の障害である損失エネルギーを無くすことができ,高速回転をすることができる.また,今日では,実用化に向けてエネルギー貯蔵用のフライホイールに適用されようとしている.
|
| 磁気浮上・磁気軸受技術 |
磁気軸受
|
|
ロータを非接触で支持
潤滑油不必要 軸受磨耗なし 騒音が少ない |
 |
 |
| 超高速回転の実現 |
フライホイール |
|
|
| 超高速回転を実現するためには... |
|
|
| 高次弾性モードの危険速度通過問題 |
 |
| 剛体モードのみを考慮したモデルノッチフィルタを用いた制御系 |
 |
| スピルオーバ不安定 |
 |
| 弾性モードを考慮した制御系 |
|
|
 研究の目的 研究の目的
| ■ |
フレキシブルロータにおける高次弾性モードを考慮したモデルの作成 |
| ■ |
PID制御とLQ制御を組み合わせたPID包含LQ制御を適用し、運動と振動の制御 |
|
|
 制御対象構造物 制御対象構造物
|
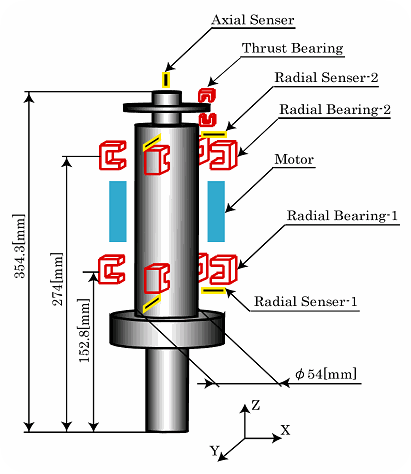
寸法,重量を述べる.
センサー及び,磁気軸受はX,Y軸方向にそれぞれ2個ずつ,Z軸方向に1個ずつ取り付けられている.
簡略化のため,現段階ではロータのダイナミクスはX軸方向のみを考える.さらに,ジャイロ効果,コイル特性,電磁石等の非線形性は考えないものとする.
|
|
 |
 |
|
|
 振動モード形 振動モード形
|
 |
 |
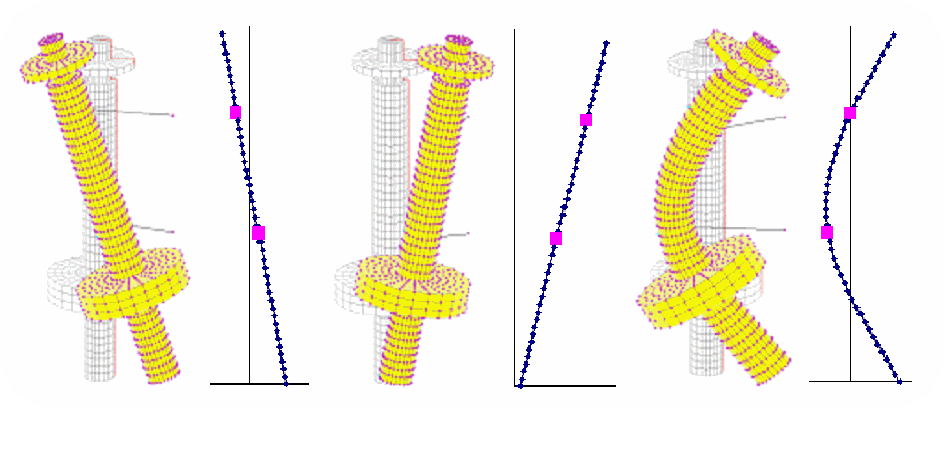
このロータを有限要素解析ソフトNASTRANを用いて解析した時の振動モード形及び固有振動数はこのようになる.
本研究では1次から3次モードまでを制御対象します.1次,2次,3次・・・.
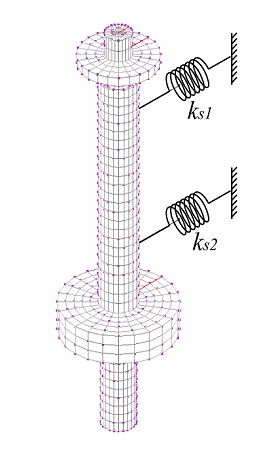
ここで,磁気軸受による制御入力をサーボ剛性として考え,サーボ剛性を含んで解析を行った.
我々は制御対象を3次までとしたので,3質点モデルを作成します.
モデリングポイントとして磁気軸受の設置位置と1次モードの最大振幅点であるロータの最下点を選択した.
|
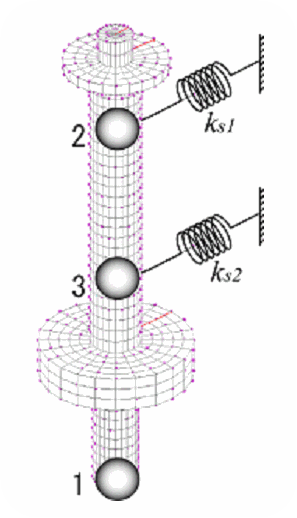 |
|
 低次元化物理モデル作成法 低次元化物理モデル作成法
一般の構造物は無限次元を有する分布定数系であり,振動制御を行う際,集中定数系の物理モデルに低次元化しなければならない.物理座標系の質量行列M および 剛性行列K はこのように表せる。
しかし、現段階では集中定数系モデルは得られていないので、当然Φも未知数となる。
そこで、先ほど示した振動モード形から各質点のモード成分を読み取り、等価質量同定法により得られた等価質量によって正規化することで、このような「仮の正規化モード行列」を得ることができる。
|
集中定数系モデル

|
  未知数 未知数 |
| 振動モード形の各質点のモード成分 |
 質量感応法 質量感応法 |
 |
この仮の正規化モード行列Φは、分布定数系の振動モードからの固有モード成分で作られているので、この式の右辺は対角行列とはならず、このように非対角要素が現れてしまいます。
そこで、この非対角要素をゼロに収束させるような修正を考えます。
まず、非対角要素を誤差関数εと定め、このように置きます。
また正規化モード行列の各成分に対する誤差関数の感度行列はこのようになります。
|
|
| あとは工事中です! |
|
|
|
|
|
|
|
  |
![]()