近年、国際宇宙ステーション（ISS）に見られるように、宇宙環境開発が活発になりつつあります。これに伴い、宇宙構造物の振動が問題となります。宇宙構造物の振動発生の原因は、打ち上げコストの削減・省エネルギー化による軽量化による剛性の低下、太陽光の当たる場所とあたらない場所での激しい温度差による熱応力、スペースデブリの衝突、さらに内部機器から発生するものが考えられます。 　発生した振動による影響として、太陽電池パネルの性能の低下、発生した慣性力による構造物の姿勢の変化、通信機器の影響、構造物の破損の可能性が考えられます。さらに宇宙空間では減衰要素が少ないため、一度発生した振動は減衰しにくくなります。そのため外部から振動制御を行う必要があります。 この研究は宇宙空間にある柔軟構造物の振動制御に関する新しい方法論を提案し，それを模型装置によって実証することを目的としております。宇宙ステーションには典型的な柔軟構造物である太陽パドルは不可欠ですが，これが一度振動するとステーション全体が振動し地上との通信を阻害します。そこで，私の研究では複数の太陽パドルを振動制御の対象に選び，これが並列に配置された時の相互反力を利用して振動を止めようとしております。通常，同じ振動特性を持つ柔軟構造物の相互反力を利用して振動制御することは困難とされておりますが，私の研究では反力を取る場所の工夫によってこの問題を解決しております。この方法によれば，大きな反力が得られるので大きな制御力が得られ，また曲げや捻れの多数の振動モードが制御できます。目下，２枚の太陽パドルに見立てた柔軟構造物を設計製作し，基礎的な制御によって，この考え方の有効性を実証した段階です。これから本格的な多モード制御に入ろうとしております。

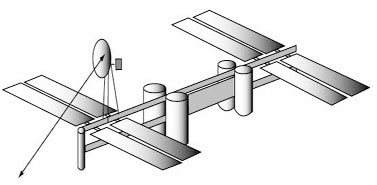
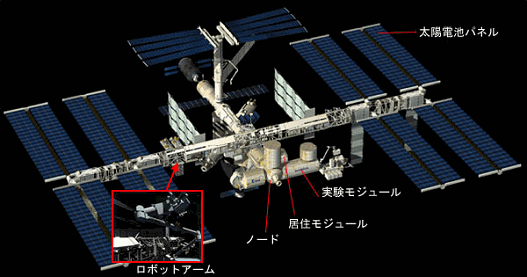
上の図は宇宙ステーションのイラストです。　　　　　　
アンテナが揺れると地球と正確な通信ができかねません。
この問題の解決に向けて目下研究を行っています。　　　

まず、実験の背景には、近年の宇宙環境利用は益々活発化の傾向にあり、宇宙用構造物は様々な軽量化・柔軟化が進んでいる事が挙げられます。 　宇宙は無重力かつ真空な空間であり、そこにおかれた構造物は、一度振動が発生すると、減衰は殆ど生じないので、何らかの方法で制振を行わない限り振動は減衰しないことになります。よって、効率的に振動を制御するために新しい方法で試しています。 　そこで本研究では、柔軟宇宙構造物として、宇宙ステーションの太陽パドルに見立てた同じ特性の２枚の薄い平板を直列に並べ、その振動制御を行うことにしました。この方法を利用したのはは、構造物の相対運動を利用するので制振装置の出力が小さくても、大きい制御効果が得られると考えられるからです。 　また、実験装置の設計、組み立て、プログラムを組む事などは自分たちで考えて、実験をしました。
振動制御 太陽電池パネル ２枚の薄いアルミ平板に見立てる 相互作用力制御方式 更に，１軸回転自由度を持つドラムに構造物 を取り付けることで宇宙ステーションの動きを 再現する．
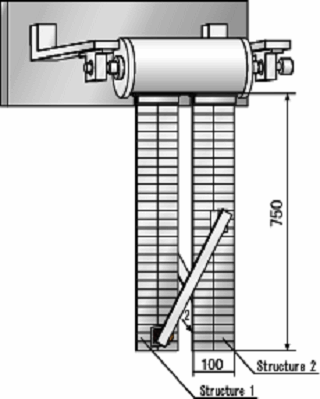
			Φ180×300 t=20[mm] 外径180ｍｍ、長さ300mm、厚さ20mmの１軸回転自由度を持つドラム
			750×100×2[mm] 縦750mm、幅100mm、厚さ2mmの太陽電池パネルに見立てた2枚のアルミ平板
			クロスアームアクチュエータ クロスアームアクチュエータはこのように設置してある
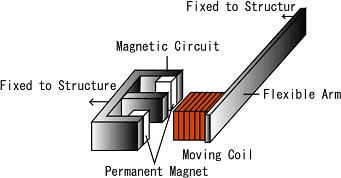			電磁アクチュエータ
			制御力を発生させるための電磁アクチュエーターを平板とアームの先端に取り付けました
実験モード解析
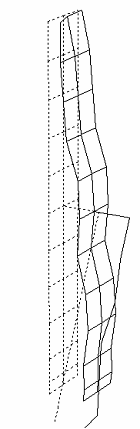
剛体モード	柔軟体モード
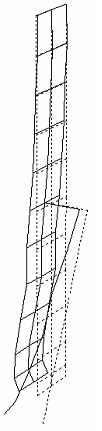
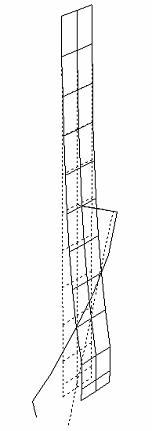
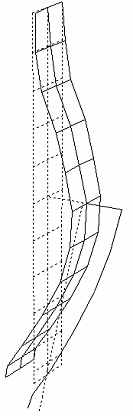
1次モード 0.625 [Hz]	2次モード 1.973 [Hz]	3次モード 5.25 [Hz]	4次モード 13.97 [Hz]	5次モード 30.92 [Hz]
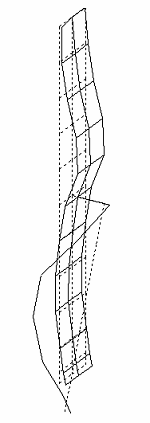
制振対称構造物の1次から5次のモード形は上記のようになっています． 1次モードはドラムの剛体モード、２次モードは平板曲げ1次モード・3次モードはアーム曲げ1次モード・4次モードは平板曲げ2次モード、5次モードはアーム曲げ２次モードとなっています． 本研究では、パネルの振動制御を目的としているで、制振対象とするモードは2次から4次までとします． 制振対象モードの各最大振幅点の位置をモデリングポイントとし，3質点に低次元化します。このモデリングポイントは平板とアームの先端、アームの取り付け位置となっています．
回転運動を含む振動制御モデルの作成法
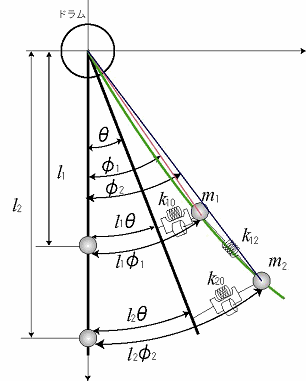２質点モデル			剛体モデル　　＋ 回転運動	柔軟体モデル 振動
ここでは、運動は振動に影響を与えるが、振動は運動に影響を与えないと仮定します． モデルは剛体モデルと柔軟体モデルをあわせたものであり，剛体モデルは回転運動を，柔軟体モデルは振動をそれぞれ表しています．ここでは簡単のために2質点モデルを用います． 回転角θ、φが微小である場合，回転方向と並進方向の関係は上記に表すことができます。 （質点m1を例に取りますと、回転方向と並進方向の関係はX1=L1･φ1で表すことができます．質点m2についても同様になります．これにより回転方向の運動を並進方向の運動に変換することができます．） この関係を用いて，各質点について運動方程式をたて、状態空間表示します。 しかし，制御対象構造物は分布定数系であるため、振動制御モデルを作成するにあたり、集中定数系に低次元化する必要があります．
低次元化物理モデル作成法
まず、物理座標系とモード座標系の関係を説明します。モード質量行列は物理座標系の質量行列を用いて下記に表されます． （ここで，モード行列Φはモード解析によって得られた各質点のモード変位になります．） 等価質量を用いて作成した正規化したモード行列を用いると?質量行列Mと剛性行列Kはこのように表されます。したがって、物理座標系のシステムは、それぞれのモードのモード行列、等価質量、固有振動数によって決定することができます。
＜物理座標系とモード座標系＞ モード質量行列
				M ：物理座標系の質量行列 Φ ：モード行列 mi：モード質量
正規化モード行列
				φi：固有ベクトル mi ：モード質量（等価質量）
質量行列M・剛性行列K
				M：物理座標系の質量行列 K：物理座標系の剛性行列 Φ：正規化モード行列 Ω：固有振動数行列
＜誤差関数の感度を用いた固有モードの修正法＞
誤差関数の感度を用いた固有モードの修正法について、2自由度系で説明します。 この時点では物理座標系のシステムのモード行列は未知量であるため，仮の固有モード行列を分布定数系のモード形によって作成します。質量行列Mは先の式よりこのように表され，仮の固有モード行列をもちいてこのように表されます。この式を満たす条件としては両辺を対角行列にする必要があります。 そこで，非対角要素を誤差関数εとして定義し、εを０にします。
→
誤差関数ε			2自由度系	連続系のモード形から任意のモデリング点の成分を抽出した仮の固有モード行列
固有モードΦに対する誤差関数εの感度関数をこのようにおきます。固有モードΦの修正ベクトルを用いると、誤差関数εはこのように表されます。これを最小ノルム解を用いた一般化逆行列により修正量を求めます。この修正量を用いて反復計算を繰り返すことにより誤差関数εを０に収束させることができます。これにより得た修正された固有モードφより，質量行列M、剛性行列Kを求めることができます。
Φに関するεの感度関数			Φの修正ベクトル
最小ノルム解を用いた一般化逆行列
低次元化物理モデル
低次元化物理モデル作成法により得た各物理パラメーターは下記のようになり，低次元化物理モデルは下のような図になります。各減衰要素は，構造物の内部減衰、アクチュエータの磁気減衰をそれぞれ表しています。この低次元化物理モデルは柔軟体モデル，つまり振動を表現するモデルとなっています。
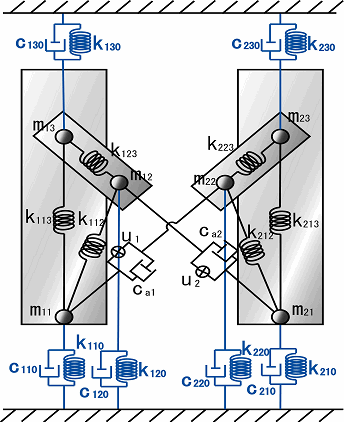			物理パラメータ mi1=0.197 [kg]　 mi2= 0.084 [kg] mi3= 0.242 [kg] Ki12=0.256×102 [N/m] Ki13=5.049×102 [N/m] Ki23=1.382×102 [N/m] Ki10=-2.700×102[N/m] Ki20=-1.039×102[N/m] Ki30=1.400×103 [N/m] Ci10=0.050 [Ns/m]　 Ci20= 0.010 [Ns/m]　 Ci30=0.150 [Ns/m]　 Cai=0.250 [Ns/m]
剛体モデルの作成法
次に，回転運動を表現する剛体モデル作成法について説明します。ドラムとパネルを物理振子として考え、その時刻暦応答によって作成します。時刻暦応答より振幅比を読み取り，対数減衰比を求め，各係数を求めます．ドラムの運動方程式は下ように表され，各係数は下記のようになります．ここで，慣性モーメントは理論的に求めます。
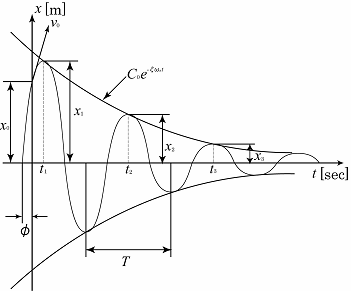			対数減衰比 ドラムの運動方程式
制御系設計
柔軟体モデルを作成する際に，分布定数系から集中定数系に低次元化したために，無視した高次モードがスピルオーバを引き起こす可能性があります．そこで，2次系のローパスフィルタを用いて高次の制御信号をカットし、スピルオーバを防止します．（下図は，制御対象にフィルタを組み込んだブロック線図になります．）
Second-order Low Pass Filter　　　　　　　　　　　　　　Control Object 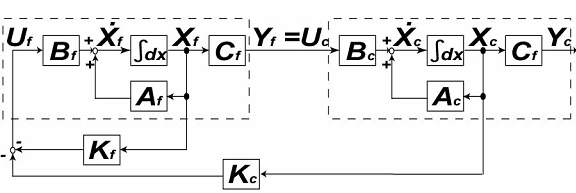制御対象に２次系ローパスフィルタを 接続したブロック線図
Kf、Kcはそれぞれのフィルタと制御対象のフィードバックゲインであり，これはLQ制御理論を用いて求めます． ローパスフィルタを組み込んだ状態方程式と観測方程式は下のようになります．
状態方程式　 観測方程式
制御シミュレーション
設計した制御系を用いて行った，制御シミュレーションの結果を示します． 質点13を観測し，同点を加振した際の周波数応答と時刻暦応答はこのようになります．青が非制御時，赤が制御時となっています．今回使用した重みはこのようになります． また、剛体モードは制御対象外であるが，状態変数にドラムの回転角が含まれているので，剛体モードに重みがかからないようにするために準最適制御理論を用いました．周波数応答を見ると，剛体モード以外の共振ピークが低減していることがわかります． また，時刻暦応答を見ると、振動が約3秒と速やかに収束していることがわかります．ここで，定常的な振動は，非制御対称の剛体モードの残留振動となっています．
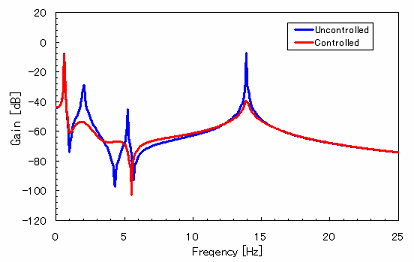周波数応答		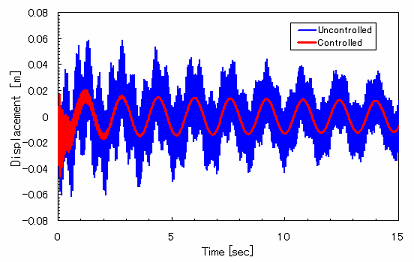	時刻暦応答
質点13を観測・質点13を加振
実験装置
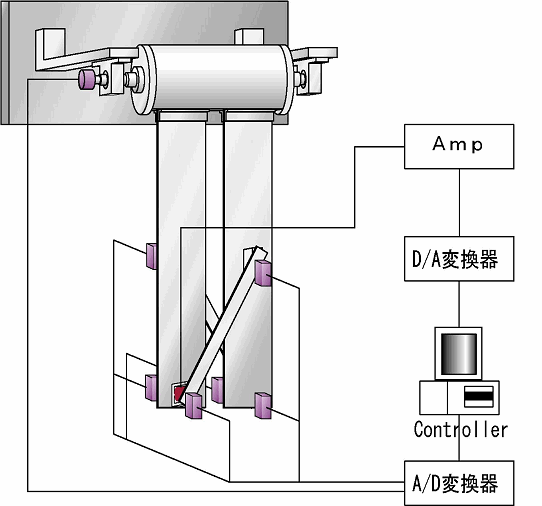
制御実験に用いる実験装置について説明します． パネルとアームの各点の変位はレーザー変位センサによって、ドラムの回転角はポテンショメータによって測定され，A/D変換器を通してからコントローラーに入力させます．コントローラー内部において，測定した変位と角度を微分することで速度と角速度を算出します．コントローラーによって算出された制御信号は、D/A変換器、アンプを通して，アクチュエータに入力され制御力を発生させます．
実験結果
制御実験結果を下記に示します． 制御シミュレーション同様，質点１３を観測し，同点を加振したときの周波数応答と時刻暦応答はこのようになります．ここで用いた重みは制御シミュレーションと同様のものとなり，準最適制御理論を用いました．青が非制御時，赤が制御時となっています。 制御シミュレーションと同様，周波数応答では剛体モード以外の共振ピークが低減しています。時刻暦応答では振動が約3秒と速やかに収束していることがわかります．定常的な振動は，非制御対象の剛体モードの残留振動となっています．
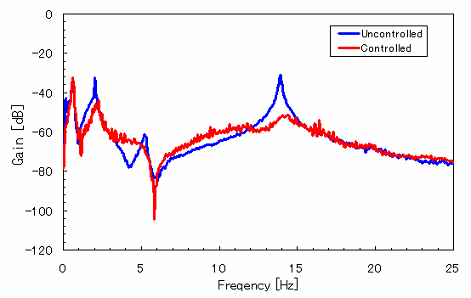周波数応答		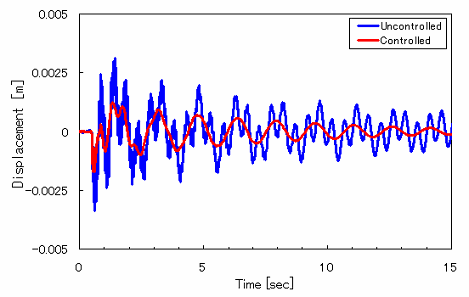	時刻暦応答
結　論
■相互作用力制御方式を用いた本手法は，剛体回転自由度を有する制御対象構造物の振動制御においても有効であることが，振動実験結果より実証できた． ■制御対象構造物の剛体回転運動と，柔軟体の振動を同時に表現する振動制御のためのモデルを作成し，その有効性を実証した．

Go to study