大変形下での応力−歪の関係（大変形での弾塑性構成方程式）を定式化するためには幾何学的な非線形挙動を可能な限り正確に測定する必要がある。すなわち、大きな変位を測定すると同時に微小な変位も正確に測定する必要がある。そこで、微小変形から大変形にわたって、引張とねじり変形を同時に加えることのできる多軸試験機を作成し、弾塑性負荷実験を行なっている。

　試験片の材質は、大変形を生じさせるために延性材料の中でも、特に純銅（タフピッチ銅＜99.99％＞）を採用している。なお、試験片は、円筒形状であり、加工後焼きなまし（加熱後炉中冷却）の処理が施されている。

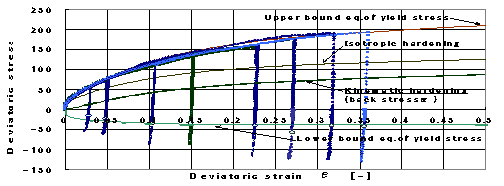
図4は、引張の予変形(歪の値で3%〜36%)を加え、その後圧縮負荷を与えた後に除荷(再度引張方向負荷)を行なった一連の変形過程で得られる実験値を示した図である。偏差応力の曲線は、引張実験の値から歪硬化係数を定めて得られたものある。一方、圧縮側降伏応力 は、圧縮側降伏限界値○とほぼ一致するように定めたものであり、これより降伏球面の膨張を表す等方硬化(isotropic hardening)による応力と、降伏球面の中心位置の移動を表す背応力α(back stress)が、図中の曲線の様に推定できる。

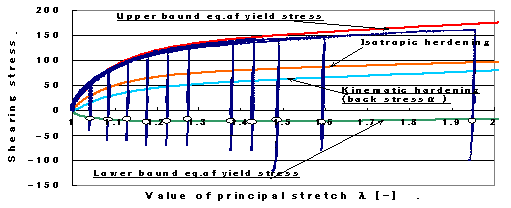
図5は、剪断変形(ねじり角で15deg〜270geg)の実験値を示した図である。そして、これらの実験値と自然歪理論を基に引張の実験結果から解析を行った逆剪断側の降伏限界値の曲線とがほぼ一致していることから、本理論の合理性が検証できる。

　　本研究では、更に変形に伴って発生する異方性についても検討を行っている。ここでは特に引張や剪断による大きな予変形を受けた材料に対して、多軸負荷実験を行い弾性係数Gの異方性の存在を確認している。

　本研究では履歴の異なる予変形を与え、予変形の負荷履歴と降伏曲面の異方性の発達の関係を調査している。
　その際の降伏応力の決定方法の概略を図6の偏差主応力-偏差主歪線図に示す。この図では、緑色の曲線が試験片に最初に与える大きな予変形を表し、この予変形の最終状態から再度負荷を加え再降伏する一連の過程が示されている。この時、予変形の降伏応力値が明らかであることから、再降伏時の降伏応力値も既に確定しており、それは図中のB点で表わされることになる。このB点の近傍における偏差主応力は、緩やかな曲線になるが、本研究ではその曲線を(1)式に示す実験式で表し、実際の偏差主応力-偏差主歪線図上の実験値に一致する様に式中の係数a,b,c,d,をLM法、即ち、非線形最小二乗法を用いて決定する。更にこの式を微分することで、B点での接線係数を(2)式のように求めることができ、歪硬化係数hも(3)式のように求めることができる。本研究では、この降伏時の接線係数と同一値となるところの応力を降伏応力と推定することにする。この図では一例として逆向きに負荷を加え続けた際の降伏応力が、B点と同一値の接線係数である図中のD点で表されている。一方で残留歪に基づく耐力による降伏応力は、図中の残留歪e1rを用いてC’点で表され、本研究とは異なった値となる。

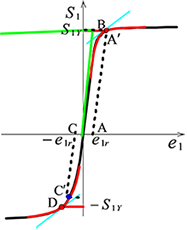
Fig. 6 Principal deviatoric stress-strain diagram

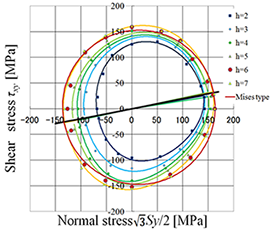
Fig.7 Shape of yield surface (Tension after shear)

　予変形の変形履歴が降伏曲面の形状の異方性に及ぼす影響を調べるために、一例として、剪断後に単軸引張の予変形を与える場合の降伏曲面の形状を図7に示す

　本研究では、図8に示す様に大きな予変形を試験片に与えた後に、更に繰り返し荷重を試験片に与えて各サイクル内の降伏応力を測定し、繰り返し数の増加に伴う降伏応力の推移を調べている。一例として、大きな剪断を与えた後の剪断の繰り返し荷重下で得られる繰り返し数Nと降伏応力の関係を図9に示す。図中の赤色の破線が本研究の結果を青色の破線が従来の残留歪に基づき降伏応力を決定する耐力の結果を表している。この図より、耐力の結果は、本手法の接線係数に基づき推定した降伏応力に比べて低い値となることが確認できる。

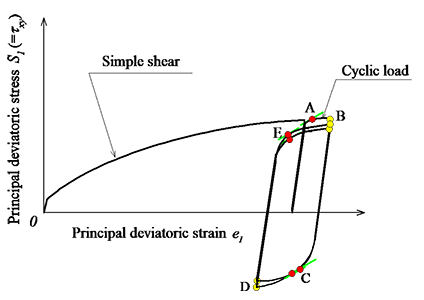
Fig.8 Cyclic load after pre-deformation of simple shear

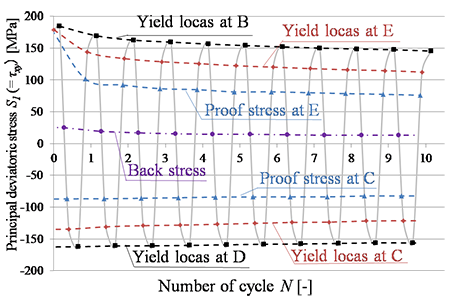
Fig.9 Change of yield stress with the cyclic load (λ=1.9[-] ^⊿e₁=0.006[-])

研究テーマのページに戻る