大変形理論を考慮した円板の弾塑性解析に関する研究

Large Deformation Analysis of a Circular Plate

　一般に円板の極限解析では降伏後に形成された塑性関節部を含む塑性領域は広がらず、その関節箇所でのみ塑性変形が増大することが述べられている。過去に行ってきた本研究の実験からは、塑性関節は円板の内外周から広がることが確認でき、従来の極限解析の理論には矛盾点が含まれていることが明らかとなった。更に、その実験結果からは、塑性関節が形成された後には大きな撓みが発生することが確認でき、大変形の理論を考慮して関節の変形を検討して行かなければならないことが明らかとなった。そこで、本研究では、有限変形理論を念頭に置いて弾塑性解析を進め、関節部の変形挙動を調べていくことにする。

　塑性関節の変形機構として半径方向の曲率増分と周方向の曲率増分の変形比が次式となるときに関節の変形が発達することが述べられている。

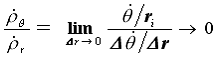　　　　(1)

　降伏(全塑性モーメント)到達時までの変形では図１(a)内の内外周の境界位置(a点、または、d点)での傾斜角が0であることを考えると、(1)式を当然満足する。しかし、降伏後の塑性解析においてはa点、d点で関節が形成され、傾斜角が有限な値を取りが存在するため、(1)式の条件を満たすためにはが∞をとらなくてはならない。これは、(1)式においてとなるときであり、塑性関節部の長さが広がらず同一の位置(a点或いはd点)で塑性変形が進行することを意味する。

　しかしながら、現実には板厚が存在し、曲率の大きさには限界があること()を考慮するとが∞にはならず(1)式で表される塑性関節部のルールは必ずしも実際の塑性変形挙動を的確に表現していないことがわかる。

　研究概要で述べたように、内外周で共に固定支持のこの支持条件では、塑性領域は大きく広がる(半径,)。そのため、関節領域はその広がった塑性領域の内部に存在する(半径,)と考えられる。
　また、有限に広がるこれらの関節領域の長さをここではそれぞれ,で表すことにする（図１(b)参照）。

図３は、負荷実験の様子を表しています。中央部に荷重(最大約9[ton]
(88.2[kN]）)を加え、荷重ごとに歪とたわみの測定を行います。
なお、円板の材質はSS400材（軟鋼）です。

Fig3.The experimental device

　図4に荷重たわみ線図が示されています。また、図5では、降伏曲面と変形点が交差している半径の位置から、塑性域の広がる位置(つまり、弾性と塑性の境界位置)が推定できます。従来の理論では塑性関節は内周の一点で生じると考えられているのに対し、荷重の増加に伴い、内周(r=98[mm])から外周に向かって塑性関節を含む塑性領域が広がっていくことがこの図の関係からわかります。

Fig.4 Load-deflection curve

　図６は、最大でまで荷重を加えたときの膜力と曲げモーメントの数値計算結果を微小変形理論と有限変形の理論に対して示し比較したものである。これらの結果から微小変形理論に基づく内力（膜力と曲げモーメント）または変形（）の方位は、有限変形理論（大変形理論）のものと比較すると差異があり、また各半径位置の値を同一荷重（最大荷重）で比較した場合、微小変形理論の値が有限変形理論に比べ大きな値となることがわかる。
　なお、これらは弾性解析であるが、参考のために材料が軟鋼材SS400の場合の降伏曲面が図中には示されている。この図で、解析結果は、最初に内周（）からこの擬似降伏曲面と交差し始め、最大荷重では半径位置（）で交差していることから、塑性領域は内周から外周に向かって徐々に広がっていることが確認できる。

研究テーマのページに戻る