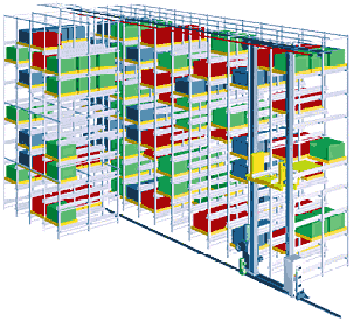
本研究が研究の対象としている搬送システムとは、自動化された工場や倉庫内において人に代わって棚などに収納された荷物を移動させる自動システムのことです。
その搬送システムの主な特徴として、こちらの搬送システム全体はこのように水平方向に，内部に設置されたこのエレベータは作業する棚にあわせて垂直方向に移動可能です。
このような駆動機構により作業効率を向上させたり、人が作業するのには非常に困難な冷凍倉庫などで、自動で荷物を運ぶ役割にあります。
そして、その構造は内部に存在するエレベータにより、このように左右対称な枠組み構造となります。

本研究の背景といたしましては、まず先ほどの搬送システムにおいて高速化、省エネルギー化などの社会的要求が挙げられます。
これらの要求を満たす方策のひとつとして機器の軽量化が挙げられますが、これは構造が柔軟なものとなり固有振動数が低下し、振動の発生が問題となります。
そこで、搬送システムにおいて自動で作業するための位置決め制御に加えて、同時に振動も制御する必要があると考えられます。

増加の傾向にある高速化・省エネルギー化の要求

軽量化による構造の柔軟化

固有振動数の低下による振動の発生

振動による作業効率の低下

運動と振動の制御が必要

そして、搬送システムの特徴として、このように荷物を搭載したり、エレベータが移動するなど制御において無視できない状態変動の影響が挙げられます。
特にエレベータが移動する場合では，搬送システム全体のパラメータが時間とともに変化します．
そこで、運動、振動制御にはロバストな制御が必要であると考えられます。
ここで，本研究では，設計の段階で考慮していない変動に対しても制御効果の劣化が少ない制御のことをロバストな制御としています．

無視できない状態変動の影響
　　・搭載質量の有無
　　・エレベータの移動

ロバストな制御が必要

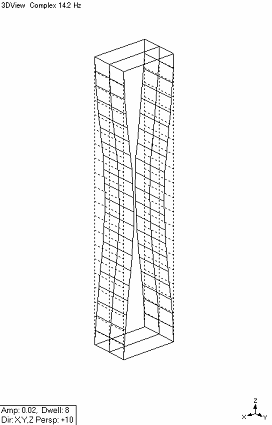
また、先ほども述べましたように搬送システムはエレベータの存在により、枠組み構造となります。
搬送システムのみならず、このような柔軟な枠組み構造には、本研究がドラミングモードと呼んでいる通常の曲げモードとは異なる振動モードが存在します。
このドラミングモードとはこちらのように左右の平板が正反対の方向に振動変位を持ちます。
本研究はひとつのアクチュエータで制御を行うため、このようなドラミングモードの振動制御を行うのは困難です。

柔軟な枠組み構造における振動制御

ドラミングモードの存在

左右反対方向に振動変位を持つ

ひとつのアクチュエータで制御不可能

そこで本研究の目的としまして、柔軟な搬送システムの位置決め運動制御と多モード振動制御を同時に実現することとします。
具体的には、まず運動と振動の制御のためのモデルを低次元化物理モデル作成法により作成します。
次に、ロバストな制御を実現できる状態フィードバック制御系LQI制御を設計し、適用します。
そして、先ほど説明した制御不可能なドラミングモードは、通常左右対称に作られる枠組み構造を左右非対称にすることで構造的に回避することを提案します。

柔軟な搬送システムの位置決め運動制御と
多モード振動制御を同時に実現

・運動と振動の制御のためのモデル作成

・ロバストな制御を実現できる状態フィードバック制御系設計

ドラミングモードの構造的回避

・構造的に制御不可能なドラミングモードを消去

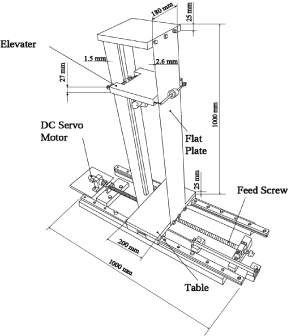
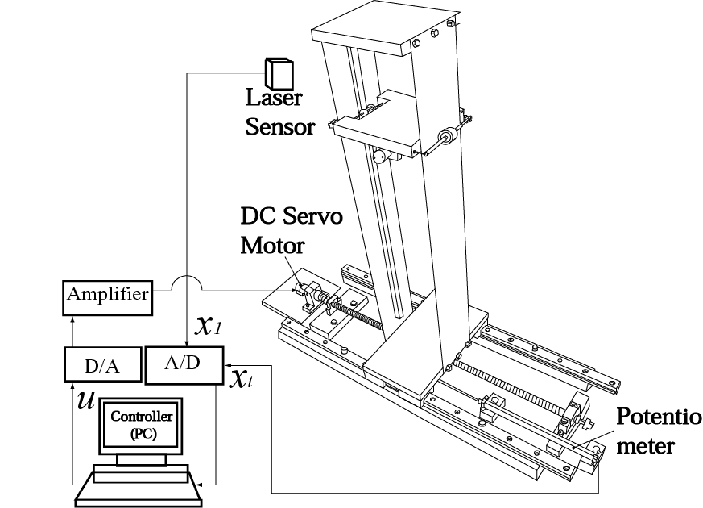
こちらは、本研究が作成し制御対象でもある搬送システムです。
こちらの土台であるテーブルにこのように平板が垂直に固定されています。
平板の寸法は高さ1000mm、幅180mm、そして左右の厚さが1.5mmと2.6mmとなっております。
本研究では、左右の平板の厚さをこのように変えることで、制御不可能なドラミングモードを構造的に回避しております。
そして、構造物全体は、DCサーボモータ、ギア、送りねじからなる駆動機構により一軸併進方向に移動可能です。

本研究は実際の搬送システムのエレベータが垂直方向に移動することを考慮し，このような状態を用意しました．制御対象物において，下部に固定している状態をノミナル状態、中間部に固定している状態がミドル状態、上部固定はトップ状態とします。

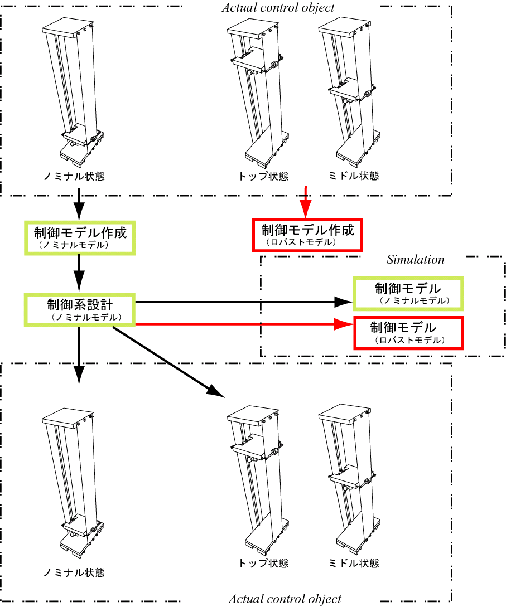まず、モデル作成を行ないます．ノミナル状態の振動モード形と固有振動数は下図のようになります。
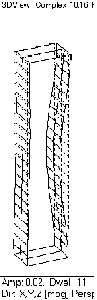
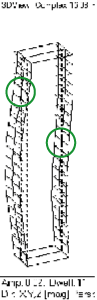
1次モードが通常の曲げモードで，2次モードは左右の振動変位が逆位相なドラミングモードです。
3次モードは通常の曲げモード、2次曲げです。
本研究では、制御対象モードを1次モード、2次モードとします。そこで非制御対象モードである3次モードにおいて、この○の部分に節が存在するため、本研究では、この節をモデリングポイントとして利用します。
また、トップ状態における振動モード形はノミナル状態と同様ですが，固有振動数は異なります。

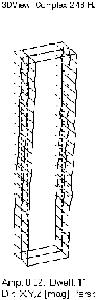nominal：1st mode:2.48 [Hz]
top：1st mode:1.85 [Hz]

2nd mode:10.2 [Hz]
2nd mode:10.5 [Hz]

3rd mode:16.1 [Hz]
3rd mode:16.3 [Hz]

次に、ミドル状態の振動モード形と固有振動数はこのようになります。
ミドル状態の固有振動数はノミナル状態とは大きく異なり、固有振動数が1次が2.12、・・・となっています。また、振動モード形もノミナル状態とは異なります。1次モードは、ノミナル状態と同様に曲げモードです。しかし、2次モードがノミナル状態ではドラミングモードであったのに対して、ミドル状態では2次曲げモードとなっています。
そして、3次モードは少し見にくいですが、上半分は通常の曲げモード、下半分はドラミングモードとなっています。この時点で、ミドル状態がノミナル状態に比べて非常に変動が大きいことがわかります。

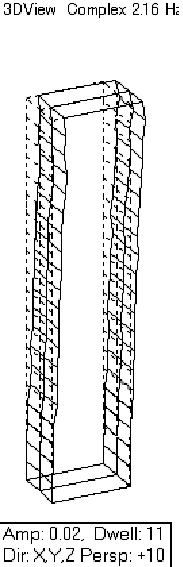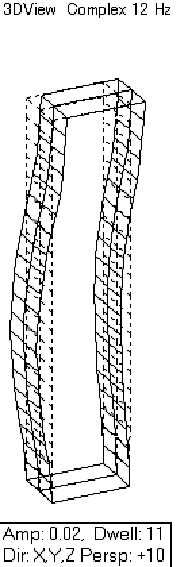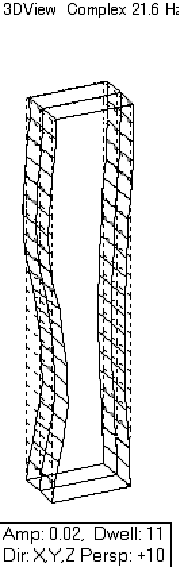1st mode:2.48 [Hz]
1st mode:2.12 [Hz]

1st mode:2.12 [Hz]
2nd mode:12.0 [Hz]

3rd mode:16.1 [Hz]
3rd mode:21.6 [Hz]

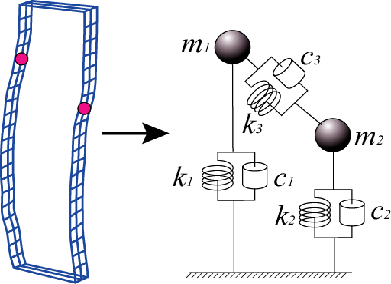
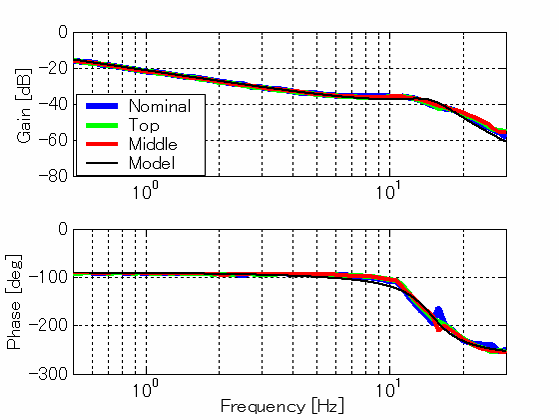
本研究は、先ほどの振動モード形を基に低次元化物理モデル作成法を用いて振動制御のためのモデルを作成しました。それぞれの状態における各パラメータはこのようになります。
まず、このノミナルモデルに対して、構造物の上部においてエレベータ分の質量増加が予想されるトップモデルでは、このように質点1の質量が増加しているのが確認できます。また、ミドルモデルではエレベータが中間部に固定してあるため、下の質点2の質量増加が大きくなっています。

ノミナルモデル

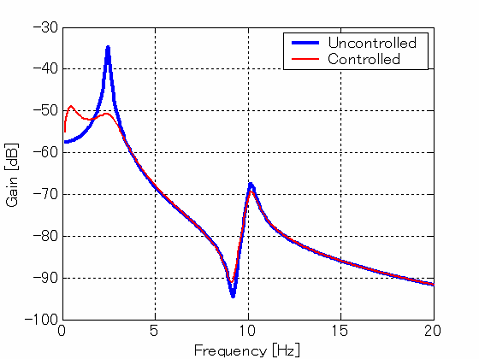非制御時，制御における質点１の周波数応答

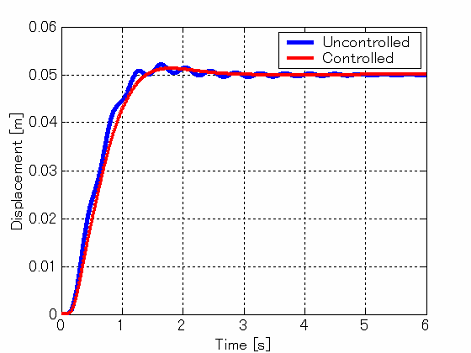非制御時，制御における質点１の時刻暦応答

ノミナルモデルのほかにロバスト性検証モデルを作成することで，実験結果だけでなく数値解析結果からも本研究におけるフィードバック制御系のロバスト性を立証

搬送システムの考えられる様々な変動に対して，ノミナルモデルの制御モデル、制御系のみで十分ロバストな運動と振動の制御を実現することができた

エレベータが移動している状態で位置決めと振動制御が可能であることを立証することで，実際の搬送システムにも本研究の成果が適用可能であることを示した